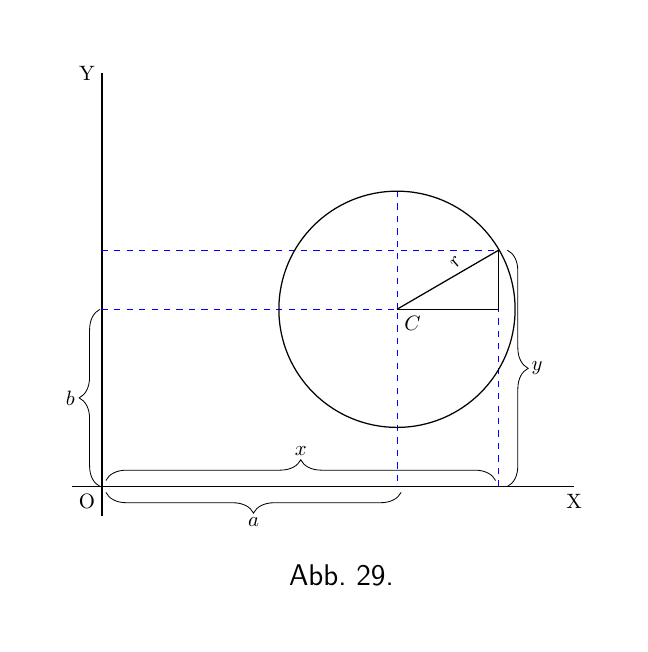
Die Gleichung für einen Kreis mit dem Radius r, dessen Mittelpunkt $C$ an dem Punkt liegt, dessen Koordinaten $x=a$ und $y=b$ sind, wie in Abbildung 29 dargestellt lautet: \[ (y-b)^2 + (x-a)^2 = r^2. \]
Dies kann umgeformt werden zu:
\[ y = \sqrt{r^2-(x-a)^2} + b. \]
Jetzt wissen wir bereits vorher, durch bloße Betrachtung der Figur, dass wenn $ x = a $, y entweder seinen Maximalwert $ b + r $ oder seinen Minimalwert $ b – r $ hat. Aber lassen Sie uns dieses Wissen nicht ausnutzen; Lassen Sie uns herausfinden, welcher Wert von x y zu einem Maximum oder einem Minimum macht, indem wir differenzieren und mit null gleichsetzen.
\begin{align*} \frac{dy}{dx} &= \frac{1}{2} \frac{1}{\sqrt{r^2-(x-a)^2}} \times (2a-2x), \\ \text{das reduziert sich auf }\; \frac{dy}{dx} &= \frac{a-x}{\sqrt{r^2-(x-a)^2}}. \end{align*}
Dann ist die Bedingung dafür, dass y Maximum oder Minimum ist:
\[ \frac{a-x}{\sqrt{r^2-(x-a)^2}} = 0. \]
Da kein Wert von x den Nenner unendlich groß werden lässt, ist die einzige Bedingung, die null ergibt,
\begin{align*} x &= a. \end{align*}
Wenn Sie diesen Wert in die ursprüngliche Gleichung für den Kreis einfügen, finden Sie \begin{align*} y &= \sqrt{r^2}+b; \end{align*}
Und da die Wurzel von $r^2$ entweder $+r$ oder $-r$ ist, haben wir zwei resultierende Werte von y
\begin{align*} \left\{\begin{aligned}y \\ y\end{aligned}\right. & \begin{aligned}= b & + r \\ = b & - r.\end{aligned} \end{align*}
Der Erste davon ist das Maximum oben; der Zweite das Minimum, unten.
Wenn die Kurve so ist, dass es keine Stelle gibt, die ein Maximum oder ein Minimum ist, führt der Vorgang der Gleichsetzung mit null zu einem unmöglichen Ergebnis. Zum Beispiel:
\begin{align*} \text{Sei }\; y &= ax^3 + bx + c. \\ \text{Dann }\; \frac{dy}{dx} &= 3ax^2 + b. \end{align*}
Gleich setzen mit null und wir erhalten $3ax^2 + b = 0$,
\[ x^2 = \frac{-b}{3a}, \quad\text{und}\quad x = \sqrt{\frac{-b}{3a}},\;\text{ was nicht möglich ist.} \]
Daher hat y weder ein Maximum noch ein Minimum.
Ein paar weitere ausgearbeitete Beispiele werden es Ihnen ermöglichen, diese interessanteste und nützlichste Anwendung der Infinitesimalrechnung gründlich zu beherrschen.
Wenn eine Seite x genannt wird, dann ist
\[ \text{die andere Seite} = \sqrt{(\text{Diagonal})^2 - x^2}; \]
Und da die Diagonale des Rechtecks notwendigerweise der Durchmesser ist, ist die andere Seite $ = \sqrt{4R^2 - x^2}$.
Dann ist Fläche des Rechtecks $S = x\sqrt{4R^2 - x^2}$,
\[ \frac{dS}{dx} = x \times \dfrac{d\left(\sqrt{4R^2 - x^2}\,\right)}{dx} + \sqrt{4R^2 - x^2} \times \dfrac{d(x)}{dx}. \]
Wenn Sie vergessen haben, wie man $\sqrt{4R^2-x^2}$ differenziert, hier ein Hinweis: schreiben Sie $4R^2-x^2=w$ und $y=\sqrt{w} $, und bestimmen $\dfrac{dy}{dw}$ und $\dfrac{dw}{dx}$; Probieren Sie es! Und nur wenn Sie es nicht schaffen, schauen Sie noch einmal hier nach.
Sie bekommen \[ \dfrac{dS}{dx} = x \times -\dfrac{x}{\sqrt{4R^2 - x^2}} + \sqrt{4R^2 - x^2} = \dfrac{4R^2 - 2x^2}{\sqrt{4R^2 - x^2}}. \]
Für Maximum oder Minimum müssen wir:
\[ \dfrac{4R^2 - 2x^2}{\sqrt{4R^2 - x^2}} = 0; \] setzen und dass ist, $4R^2 - 2x^2 = 0$ und $x = R\sqrt{2}$.
Die andere Seite ${} = \sqrt{4R^2 - 2R^2} = R\sqrt{2}$; die beiden Seiten sind gleich; die Figur ist daher ein Quadrat. In diesem Fall handelt es sich natürlich um ein Maximum, mit dem wir es zu tun haben.
Wenn $R$ der Radius und $H$ die entsprechende Höhe ist, gilt $H = \sqrt{l^2 - R^2}$.
\[ \text{Volumen } V = \pi R^2 \times \dfrac{H}{3} = \pi R^2 \times \dfrac{\sqrt{l^2 - R^2}}{3}. \]
Gehen wir wie in der vorherigen Aufgabe vor, erhalten wir:
\begin{align*} \dfrac{dV}{dR} &= \pi R^2 \times -\dfrac{R}{3\sqrt{l^2 - R^2}} + \dfrac{2\pi R}{3} \sqrt{l^2 - R^2} \\ &= \dfrac{2\pi R(l^2 - R^2) - \pi R^3}{3\sqrt{l^2 - R^2}} = 0 \end{align*}
Für Maximum oder Minimum.
$2\pi R(l^2 - R^2) - \pi R^2 = 0$, und $R = l\sqrt{\tfrac{2}{3}}$, für ein Maximum natürlich.
\[ y = \dfrac{x}{4-x} + \dfrac{4-x}{x}. \]
Wie erhalten:
\[ \dfrac{dy}{dx} = \dfrac{(4-x)-(-x)}{(4-x)^2} + \dfrac{-x - (4-x)}{x^2} = 0 \]
für Maximum oder Minimum; und
\[ \dfrac{4}{(4-x)^2} - \dfrac{4}{x^2} = 0 \quad\text{und}\quad x = 2. \]
Es gibt nur einen Wert, also nur ein Maximum oder Minimum.
\begin{align*} \text{Für}\quad x &= 2,\phantom{.5}\quad y = 2, \\ \text{für}\quad x &= 1,5,\quad y = 2,27, \\ \text{für}\quad x &= 2,5,\quad y = 2,27; \end{align*}
Daher ist es ein Minimum. Es ist aufschlussreich, den Graphen der Funktion zu zeichnen.
Es wird hilfreich sein, den Graphen zu zeichnen.
Differenzieren ergibt sofort
\[ \dfrac{dy}{dx} = \dfrac{1}{2\sqrt{1+x}} - \dfrac{1}{2\sqrt{1-x}} = 0 \]
für Maximum oder Minimum.
Da $\sqrt{1+x} = \sqrt{1-x}$ und $x = 0$, die einzige Lösung ist.
Für $x=0$, $y=2$.
Für $x=\pm 0,5$, $y= 1,932$, also ist es ein Maximum.
\[ y = \dfrac{x^2-5}{2x-4}. \]
Wir haben
\[ \dfrac{dy}{dx} = \dfrac{(2x-4) \times 2x - (x^2-5)2}{(2x-4)^2} = 0 \]
für Maximum oder Minimum; und
\[ \dfrac{2x^2 - 8x + 10}{(2x - 4)^2} = 0; \]
$x^2 - 4x + 5 = 0$; wofür
\[ x = \tfrac{5}{2} \pm \sqrt{-1} \]
Lösungen sind.
Da diese imaginär sind, gibt es keinen reellen Wert von x für die $\dfrac{dy}{dx} = 0$ ist; daher gibt es weder ein Maximum noch ein Minimum.
\[ (y-x^2)^2 = x^5. \]
Diese kann, als $y = x^2 \pm x^{\frac{5}{2}}$ geschrieben werden.
\[ \dfrac{dy}{dx} = 2x \pm \tfrac{5}{2} x^{\frac{3}{2}} = 0 \quad\text{für Maximum oder Minimum}; \]
das heißt, $ x (2 \pm \tfrac{5}{2}x^{\ frac{1}{2}}) = 0 $, was für $ x = 0 $ und für $ 2 \pm \tfrac{5}{2} x^{\frac{1}{2}} = 0$ erfüllt ist und auch für $x=\tfrac{16}{25}$. Es gibt also zwei Lösungen.
Zuerst nehmen wir $x = 0$. Wenn $x = -0,5$, $y = 0,25 \pm \sqrt[2]{-(0,5)^5}$, und wenn $x = +0,5$, $y = 0,25 \pm \sqrt[2] {(0,5)^5}$. Auf der einen Seite ist y imaginär; das heißt, es gibt keinen Wert von y, der durch einen Graphen dargestellt werden kann; Letztere befindet sich daher vollständig auf der rechten Seite der Achse von y (siehe Abbildung 30).
Beim Zeichnen des Graphen wird festgestellt, dass die Kurve zum Ursprung geht, als ob dort ein Minimum wäre; aber anstatt darüber hinauszugehen, wie es bei einem Minimum der Fall sein sollte, verfolgt es seine Schritte zurück und bildet einen sogenannten "Spitze". Es gibt also kein Minimum, obwohl die Bedingung für ein Minimum erfüllt ist, nämlich $\dfrac{dy }{dx} = 0$. Es ist daher immer notwendig, auf beiden Seiten einen Wert zu nehmen.
Wenn wir nun $x = \tfrac{16}{25} = 0,64$ nehmen. Wenn $x = 0,64$, $y = 0,7373$ und $y = 0,0819$; wenn $x = 0,6$, wird y zu $0,6389$ und zu $0,0811$; und wenn $x = 0.7$ ist, wird y zu $0,8996$ und $0,0804$.
Dies zeigt, dass es zwei Zweige der Kurve gibt; der obere durchläuft kein Maximum, der untere schon.
\begin{align*} \text{Fläche } &= S = 2(\pi r^2)+ 2 \pi r \times 2r = 6 \pi r^2.\\ \text{Volumen } &= V = \pi r^2 \times 2r=2 \pi r^3.\\ \frac{dS}{dr} &= 12\pi r,\quad \frac{dV}{dr}=6 \pi r^2,\\ dS &= 12\pi r\, dr=20,\quad dr=\frac{20}{12 \pi r},\\ dV &= 6\pi r^2\, dr = 6 \pi r^2 \times \frac{20}{12 \pi r} = 10r. \end{align*}
Das Volumen ändert sich mit einer Rate von $10r$ Kubiikzentimeter.
Machen Sie sich selbst andere Beispiele. Es gibt nur wenige Themen, die einen solchen Reichtum für interessante Beispiele bieten.
(1) Welche Werte von x machen y zu einem Maximum und einem Minimum, wenn $y=\dfrac{x^2}{x+1}$?
(2)Welcher Wert von x macht y, zu einem Maximum in der Gleichung $y=\dfrac{x}{a^2+x^2}$?
(3) Eine Strecke der Länge $p$ soll in 4-Teile zerlegt und zu einem Rechteck zusammengefügt werden. Zeigen Sie, dass die Fläche des Rechtecks maximal ist, wenn jede seiner Seiten gleich $\frac{1}{4}p$ ist.
(4) Ein Stück Schnur von $30$ cm Länge dessen Enden miteinander verbunden sind, wird durch 3 Stifte gespannt, um ein Dreieck zu bilden. Was ist der größte dreieckige Bereich, der von der Schnur umschlossen werden kann?
(5) Zeichnen Sie die Kurve entsprechend der Gleichung:
\[ y = \frac{10}{x} + \frac{10}{8-x}; \]
Bestimmen Sie $\dfrac{dy}{dx}$, und leiten Sie den Wert von x ab, der y zu einem Minimum macht und bestimmen Sie den Wert von y im Minimum.
(6) Wenn $y = x^5-5x$, finden Sie heraus, welche Werte von x y zu einem Maximum oder einem Minimum machen.
(7) Zeichnen / Fügen Sie ein Quadrat wird in ein bestehendes Quadrat ein. Wann ist das innere Quadrat am größten?
(8) Zeichnen / Fügen Sie einen gegebenen Kegel, dessen Höhe gleich dem Radius der Basis ist, in einen Zylinder
(9) Zeichnen / Fügen Sie eine Kugel in einen Zylinder
(10) Ein kugelförmiger Ballon nimmt an Volumen zu. Wenn, wenn sein Radius r cm beträgt, und sein Volumen mit einer Geschwindigkeit von 4 Kubikzentimeter pro Sekunde zunimmt, mit welcher Rate nimmt dann seine Oberfläche zu?
(11) Zeichen / Fügen Sie in eine gegebene Kugel einen Kegel ein, dessen Volumen maximal ist.
(12) Der Strom $C$ einer Batterie, die aus $N$ gleichen voltaischen Zellen besteht, ist $C=\dfrac{n \times E}{R+\dfrac{rn^2}{N}}$, wobei E, $R$, r Konstanten sind und n ist die Anzahl der in Reihe geschalteten Zellen. Bestimmen Sie das Verhältnis von n zu $N$, für das der Strom am größten ist.
(1) Min.: $x = 0$, $y = 0$; max.: $x = -2$, $y = -4$.
(2) $x = a$.
(4) $25 \sqrt{3}$ Quadratzentimeter.
(5) $\dfrac{dy}{dx} = - \dfrac{10}{x^2} + \dfrac{10}{(8 - x)^2}$; $x = 4$; $y = 5$.
(6) Max. für $x = -1$; min. für $x = 1$.
(7) Verbinden Sie die Mittelpunkte der vier Seiten.
(8) $r = \frac{2}{3} R$, $r = \dfrac{R}{2}$, kein max.
(9) $r = R \sqrt{\dfrac{2}{3}}$, $r = \dfrac{R}{\sqrt{2}}$, $r = 0.8506R$.
(10) Mit einer Rate von $\dfrac{8}{r}$ Quadratzentimeter pro Sekunde.
(11) $r = \dfrac{R \sqrt{8}}{3}$.
(12) $n = \sqrt{\dfrac{NR}{r}}$.